Qing Yang: Today we have an unusual guest – Tombos from GTO Wizard. If you've attended his seminars or read his discussions on the poker forums, you know that Tom has a deep understanding of poker theory. I decided to test it out by asking six difficult bet sizing questions.
Tombos: We agreed that the questions in this test will be as difficult and tricky as possible – as difficult as those that I asked Qing Yang on my channel!
QY: Well, are you ready for the most difficult test of your life?
TV: Let's go!
QY: Okay, first question.

The button raises and the big blind calls. One of the reasons big bets are common on flops like is the huge nut advantage of the button. And what will change if you remove all combinations stronger than top pair from the button's range?
A. The c-bet frequency will remain the same, the sizing will decrease
B. The sizing will remain the same, but the frequency will decrease.
TV: Funny question. Usually in this spot the solver wants to overbet or check. I've always said that sizing is dictated by the weight of the nuts. And now you deprive us of this advantage. Intuitively, it seems that this should lead to a decrease in sizing. This is an argument in favor of the first answer. Wait a second! After all, there is something else: on the flop of , hands like not interested in small bets because they don't need protect against equity from overcards. I wonder what will be more important here?
Perhaps I will answer B – the sizings will remain, but the frequency of bets will decrease. I think the solver will continue to choose overbets with strong top pairs remaining in its range, but will do this much less frequently. B is my final answer.
QY: And that's the correct answer! Impressive!
Here's what the button's strategy looks like with a standard range: when you give him a choice of four sizings, he always chooses the largest.
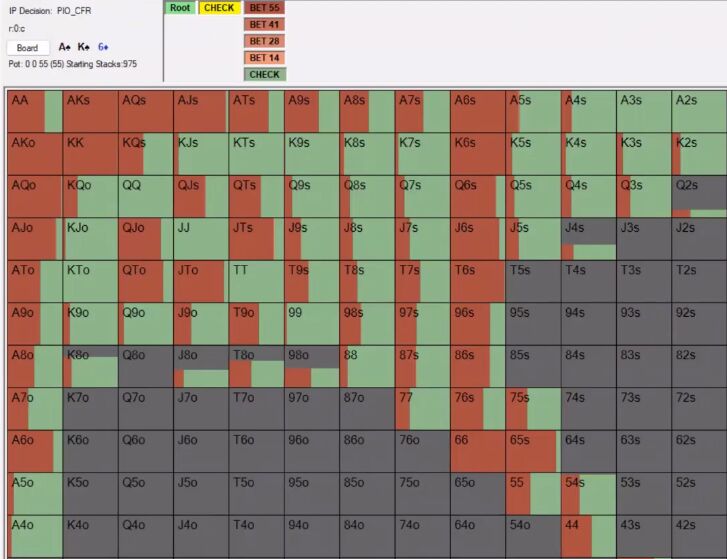
And here is the strategy without two pairs and sets. As you rightly predicted, the solver still wants to check and overbet, and bets a lot less often.

You're also right that the button doesn't have any hands on this texture that would benefit from a small size. As has about 60-70% equity, but they only fold hands that don't have direct outs. As a general rule, if we're not particularly profitable betting with marginal holdings, we need to increase our bet sizing as the c-bet range polarizes sharply. The equity of strong top pairs is over 80%, and you definitely need to bet more with them.
Let's move on to the second question.

In a situation where we only have the nuts and air in our range, the nut hands tend to go all-in. However, it is important to decrease the sizing when
A. Not enough bluffs in our range
B. Our nut holdings are blocking Villain's calling range
C. Both reasons are right
D. Both are wrong
TV: Okay. Yes, usually with a highly polarized range on the river, we want to bet all-in, and on earlier streets we want to set up a future all-in with exponential bets. A little clarification: are our nuts blocking our opponent's entire calling range, or just part of it?
QY: Only a part.
TV: Okay, then I reject the first answer. If we don't have bluffs, we just take the whole pot for ourselves. If you give a solver a similar spot where we have no bluffs, it starts doing nonsense things, for example, checking behind the nuts, because the pot belongs to us anyway. I think point A can be excluded. Point B does not change the situation, because we still only have the nuts and bluffs. We may have to change the ratio of draws and bluffs, but the sizing will remain as greedy as possible. So my final answer is D.
QY: I'm glad I managed to outsmart you this time! You're right about A: if we don't have enough bluffs, it's not a mistake to go all-in. But blocking the calling range can be a reason to reduce the sizing. Yes, I was surprised too when I saw it for the first time.
Let me illustrate this conclusion with a simplified model where each player has only two hands in their range.
Board – . An out of position player has a perfectly polarized range consisting of and 76o. The player in position has only AKs and KQo – bluffcatchers: lose to aces, beat 7-high. Player stacks are 10 times the size of the pot.
I asked four types of sizings, including an overbet all-in, and came up with surprising results: aces settled on only a two-pot sizing instead of the expected overbet shoving. After all, a perfectly polar range usually maximizes expectation by going all-in!
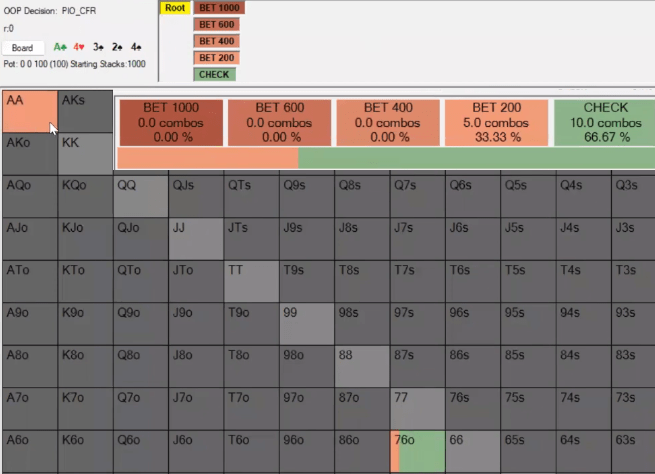
If we remove KQo from the player's range in position, he will only have one bluffcatcher left – AKs. Our nuts still interact with his calling range, but don't block anything because Villain doesn't have any other cards. And in this case, aces prefer to bet all-in.
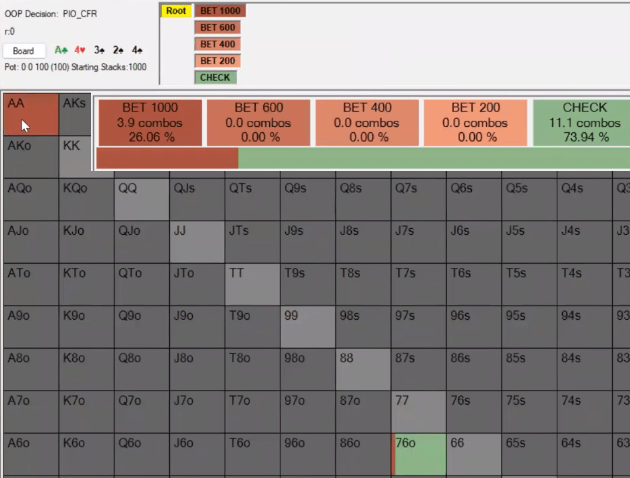
TV: What a funny model!
QY: I'm not 100% sure I'm right, but I see that when we add KQo, the EV of the larger sizes starts to decrease compared to two pots.

TB: Can you show your opponent's reaction?
QY: Of course.
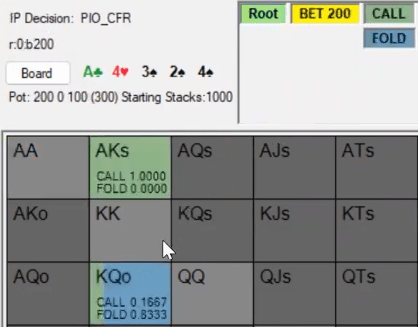
I think it's because since we're blocking a lot , it is unprofitable for us to create a situation with our bet sizing when the opponent is forced to fold all KQo. It is strategically more efficient to get some calls from this hand as well, so we have to lower our sizing.
TB: Yes, interesting. When one of the two bluff catchers blocks the opponent's draws, and the second does not, a kind of informational asymmetry arises.
QY: And it turns out that if choosing a smaller sizing can force Villain to call with a less suitable bluff catcher, this strategy may be more profitable than all-in.
Third question.

Button vs. BB again. On the K72r board, the optimal BB check-raise size is lower than usual because
A. No draws to get value from
B. It is important to be able to check-raise hands like 7x
TV: Tough question. It is obvious that on The button will bet their entire range with a small sizing. On a more dynamic board, both check-raise and check-raise defense hands are easier to pick. I think the button will have to call check-raises with many unpaired hands on K72r, so check-raises with must be profitable. So while both A and B play a role in choosing a check-raise sizing, the main reason is our desire to be aggressive with second pair. My answer is B.
QY: Right. I also prefer answer B. As you said, the button c-bets very wide (94%) with a small size. The BB, given the choice between a 3x and a 4x raise, always chooses a 3x.
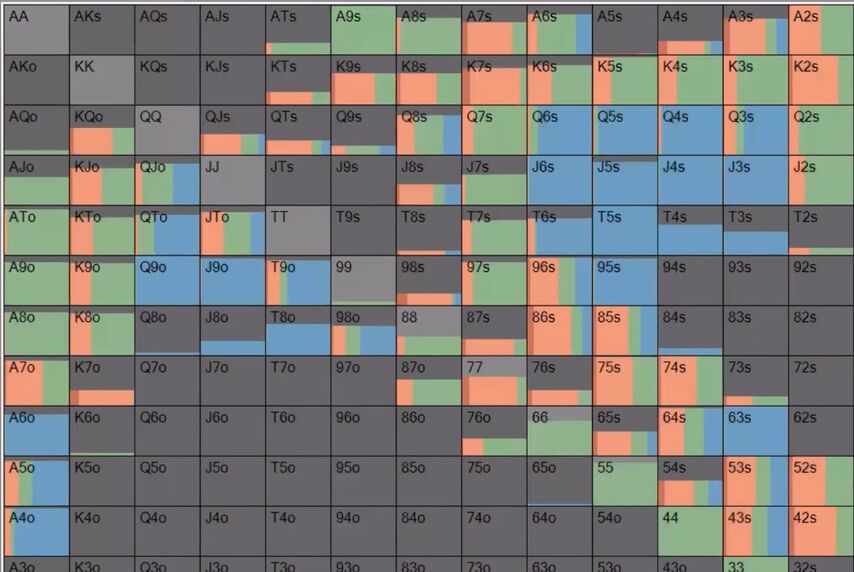
The player in position to this check-raise has to defend a very large part of his range, including many unpaired hands like T9o and JTo.
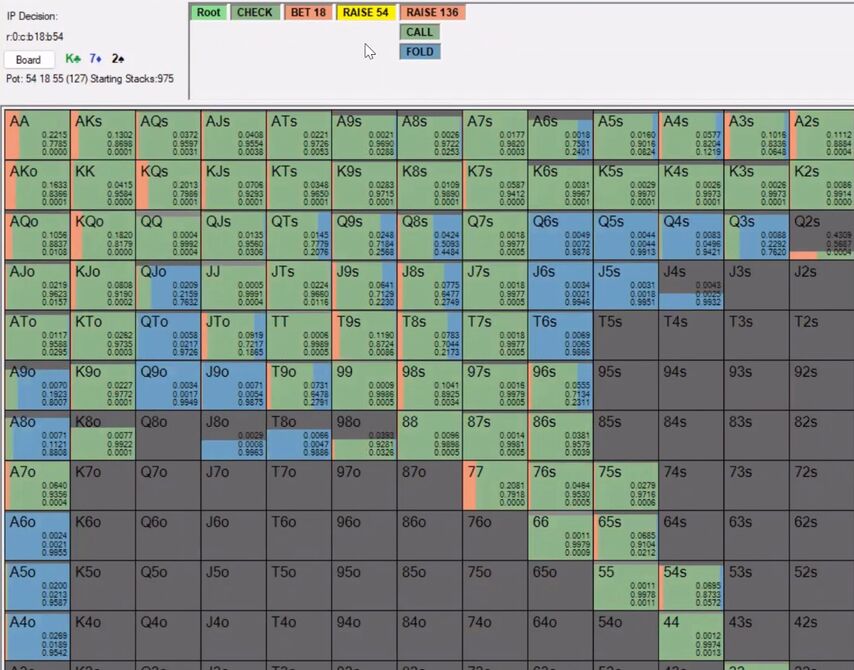
However, if you remove from the BB range all the and , he will again become interested in a more polar strategy and a larger check-raise sizing. Therefore, answer B seems more correct to me.
The same thing happens if we force the BB to only call a c-bet with and – check-raise sizing will immediately change to a larger one:
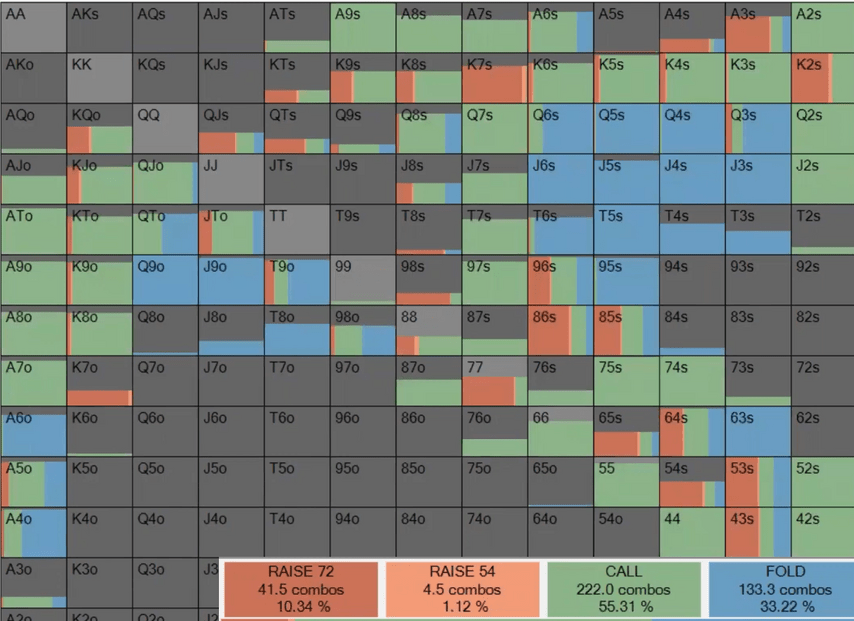
It is easier to play against a large sizing, but the solver does not operate with such concepts, it is equally easy for him to play against any strategy.
TV: Yes, I had to think a little to come up with the correct answer, but if I thought to ask myself how the strategy would change if you made the BB check with and , the answer would immediately become obvious. A beautiful example!
QY: The fourth question.

How will the bounty rule for winning a hand with 72o affect bet sizing on the river?
A. It will increase
B. It will decrease
C. It will remain the same
Just in case, I will explain what this rule is. In some cash games, if a player manages to win the hand with 72o, whether it's a bluff or showdown, all players must pay him some money.
In our question, we will assume that 72o on the river is always a bluff.
TV: What fun questions you have! Instinctively I feel that this will make the aggressor's range more polar and his sizing will increase. If Villain folds to a bluff, not only does he lose the pot, he must pay us the prize. That means, the EV of the fold becomes not zero, but negative.
Let's say the EV of folding is now -5. The aggressor should bet with such a range that Villain's marginal hands are indifferent to calling and folding with an EV of -5. To do this, the aggressor can change the ratio of draws and bluffs or increase the sizing to worsen the pot odds in case of a call. Both methods lead to the goal...
So I choose A. This is my final answer.
QY: Yes, I'm on your side. To be honest, I did not think that the EV of folding in this game becomes negative. My interpretation is that having a bounty forces Villain to call more. If in a normal game he has to call with a minimum defense frequency (MDF), he will call more often with a bounty. Because if you call according to the MDF, the aggressor will always bluff with 72o, since not bluffing has zero expectation, but bluffing this hand is positive.
Given that Villain is forced to call wider than the MDF for a certain sizing, we are able to increase the sizing with some hands. For example, let's say we have a hand that would normally bet a full pot on the river. A full pot allows you to extract maximum value from it, getting optimal equity against a calling range and not isolating yourself against too strong hands. However, with a bounty, Villain will have to call a little wider against the same sizing, so for all hands in the aggressor's range, the ideal sizing will increase slightly.
Is that logical?
TV: Yes.
QY: Well done! Three correct answers out of four. We can say that you passed the test.
Last question. It has nothing to do with bet sizing, but I find it rather interesting.

On the flush flush river, one of the reasons we bluff with a flush blocker is because it blocks our opponent's automatic calls. Will our strategy change if there are no flushes in Villain's range?
A. Flush blocker hands will continue to be preferred for bluffing
B. We will start choosing hands without a flush blocker for bluffs
C. The presence or absence of a flush blocker will not affect our selection of hands for bluffing in any way
TV: Tough question. It would seem that if we remove hands that we're trying to block from our opponent's range, we should change the strategy and bluff without a blocker on a flush. However, this coin has another side. In the solver world, blockers not only reduce the number of combinations in our opponent's range, but also help mask our own range. In both bluffs and draws, we use similar blockers, depriving our opponent of the opportunity to make perfect decisions. Therefore, I believe that since we continue to bet – and often even all-in – with flushes, the same should be done with flush blockers. Otherwise, one-flush hands in Villain's range will only block our value, not our bluffs.
My answer is A.
QY: Yes, that's right. We can't let our opponent exploit our strategy by calling with good blockers and folding bad ones. Ideally, we aim to make calls with all types of bluff catchers have an EV of zero. If our strategy allows Villain to have a high expectation group of bluff catchers and another low expectation group, this strategy is failing. The main way to avoid this is to bring cards from your value range into your bluff range.
In the example below, there are no flushes in Villain's range, our diamond blockers do not block his calling range, but for bluffs we still prefer single diamond hands. With J9o with one diamond we bluff, without – we give up.
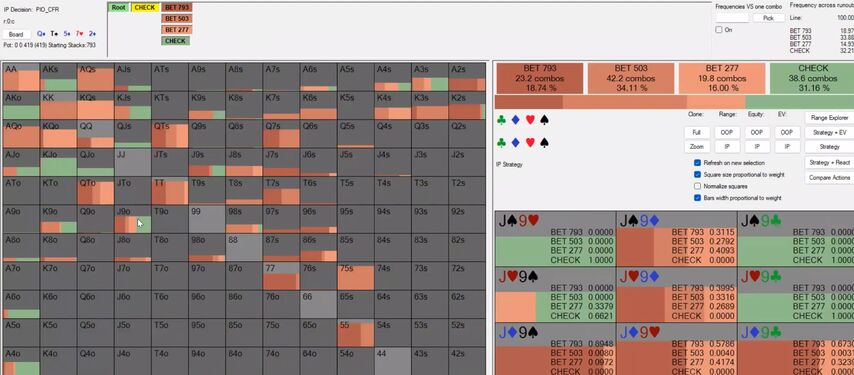
At one of the seminars, you asked the question: how do we understand why we are doing some action? Ask ourselves what opportunities the opponent will have if we do not take this action! In this case, the negative consequences of not bluffing with blockers are fairly obvious – Villain will easily be able to call with QJo with a diamond and fold QJo without a diamond.
In total, there were four correct answers out of five! Well done!










