Hello everyone, this is Phil, and today we are recording a new episode of the Phil vs. Solver column. I have the hand that Danny sent, let's look at how he played his hand and analyze the situation in which he found himself on the river. Let's compare the decision that the solver made, with the decision that I would have made. I'll also answer a question that Danny sent. This question, it seems to me, shows a certain leak in his game thinking, and the answer may be useful for him and for other players outside of the particular hand.
Let's move on to the action.
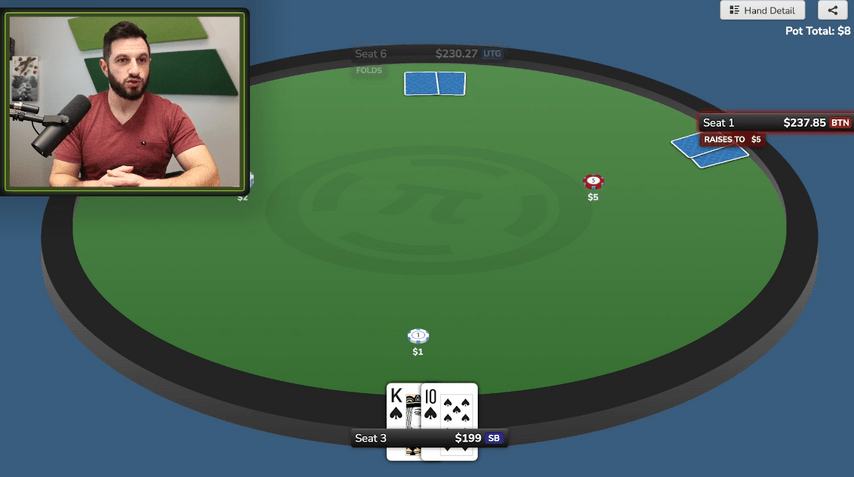
4-max and the player in first position folds, the button raises to 2.5bb. Danny 3-bets to $21 in the small blind for a little more than a 4x raise. The big blind folds, the button calls.
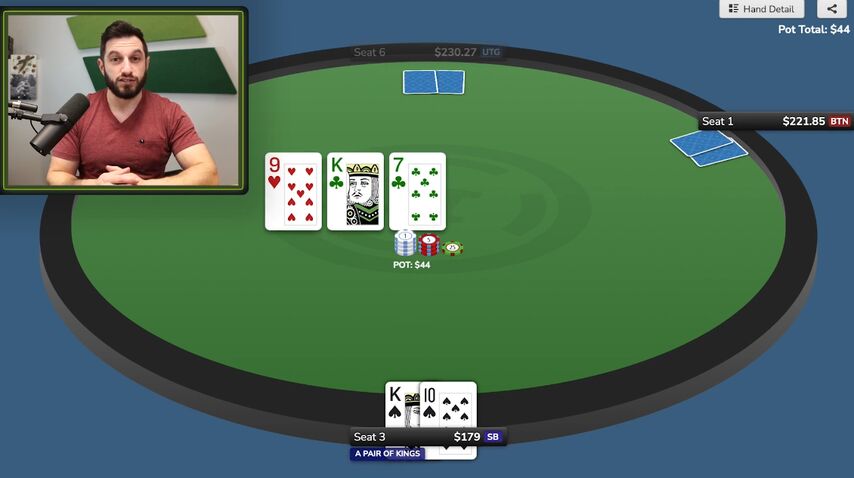
Danny checks. The button bets half pot (rake included) for $21.80. Danny calls.
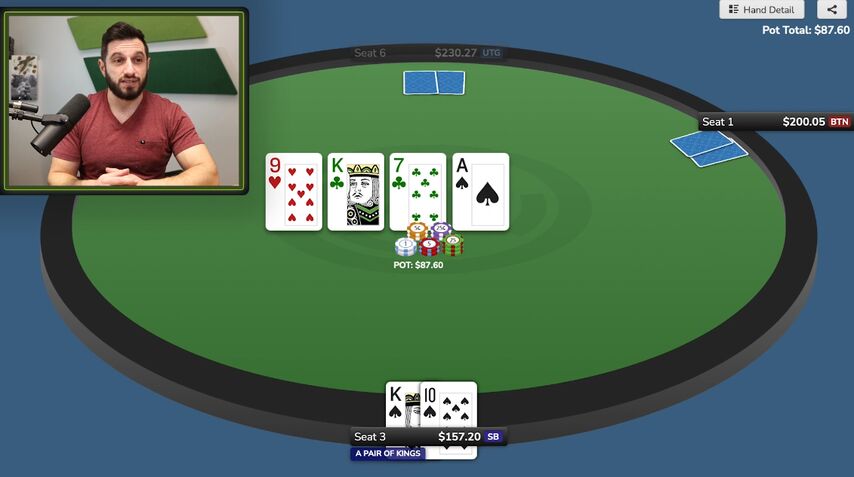
Both players check.
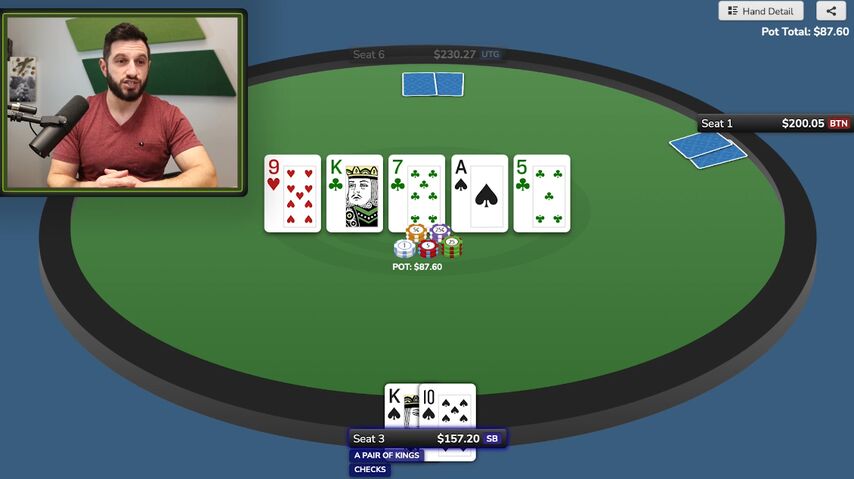
The river completes the flush and the lowest of the straights. Danny checks. The button bets $49. Danny calls.
Now let's load the solver, let's see what it says, and I will share my thoughts.
Pre-flop, there is not much to discuss, the 3-bet is standard.
On the flop , the solver only checks 20% of the time. He tends to use small c-bets most of the time, betting a quarter of the pot 57% of the time. The remaining 23% are big bets in 2/3 of the pot.
I always strive to simplify complex strategies. Here it can be done in two ways. Since we only check 20% of hands, I like to get rid of both checks and big bets and bet a quarter of the pot with my entire range. The solver mixes a big and a small c-bet with all hands, but in different proportions, which means that the expectation for these sizings is about the same. It is unlikely that we will lose much with this simplification.
Another interpretation is also possible: we completely get rid of small sizing, bet only big – 2/3 or 3/4 of the pot, betting, say, 40% of the range, and play the remaining hands from the check. If Danny is using this strategy, I like checking KTs without a backdoor flush draw. This hand is definitely not strong enough for a big bet, as it knocks out too many dominated hands from our opponent, but it greatly enhances our checking range.
By the way, in the solver strategy, KTs almost never makes a big continuation bet – there are only a few percent in the mix, with all the other KTs a small bet is made. Mostly benefitting from a large sizing are and . In general, when working with the solver, I noticed that in situations with a reduced SPR, the best top pairs and overpairs tend to increase their sizing. Intuitively, it seems logical to send the top of the range into large sizes more often, but when you have or it's not profitable for you to knock hands out of the pot that don't have direct outs against you. It is much better to keep them in the hand with a small bet, let them improve to two pair or trips.
After we checked and Villain bet half the pot (correct sizing, solver agrees), there is no choice – check-call. Yes, even here the solver finds check-raises with 4% combinations, but they can be safely ignored.

The turn is an ace. If you're wondering if the small blind has any leads on this turn, they don't: check with their entire range. You need to understand that against a bet of half the pot on the flop, we should fold a lot and , so the ace does not help us as much as you might think.
The solver suggests that the player in position often continue with a small sizing, including with . It's curious. He also has ace hands that he bluffed on the flop and can continue on the turn. Well, sets with two pair, of course, also put the second barrel.
Okay, check-check. There is nothing to discuss with KTs, this is a simple check: we were behind the opponent's value range already on the flop, on the turn some of his bluffs improved with .
River – Both the flush draw and bottom straight draw complete. With his line on the flop and turn, our opponent mainly represents , but betting for value with is still too thin, as frequent calls from and are not worth counting.
So we have a very clear check. What to do against a 60% pot bet? The solver wants to mix, but tends to fold. Our particular hand he folds 90% of the time, calls 10%.
To understand the reasons behind the fold, let's look at the button's strategy on the river: what does he bet 60% of the pot with? AQo, AJs, AJo immediately catch the eye. It looks like a significant proportion of draws with this sizing comes from hands with an ace. You know, I'm not sure that people are bluffing with on the flop as often as the solver wants to. 20% of the solver's range on the river is top pair. In my opinion, this is too much, in practice it is not worth assuming such a number of top pairs from opponents.
Another interesting thing to notice is sets. 2% of the solver's range – aces that slowplayed preflop and then on the turn. You don't have to worry about this against most people.
Lots of flushes. Everything is clear with them: betting the flop, checking the turn is a logical line, which people will often play.
With The solver never bets.
Now bluffs. Interestingly: the solver almost never bluffs with unpaired hands. Straight draws on the flop that miss are almost always checked on the river, except . Maybe it's because a jack is a better blocker than a ten? I don't know, I think they are the same. In general, 20% of the solver's range on the river is unpaired hands, and almost all of them give up and check back. I don't think people play like that.
Sometimes the solver is bluffing on the river with , but this is pretty rare.
Let me summarize.

I think Danny made a good call. First, our opponent will not have as many , how much the solver has. Secondly, a person will bluff more often with missed draws like , . There is only one moment of doubt: what if our opponent is going for value with or even with ? In this case, he will have too many value hands, and our call will be bad even with a king blocker.
The key factors for our decision are the opponent's strategy with on the flop and on the river... Will they always bet with whatever he will not bluff, and with more often plays correctly and checks back. So I like Danny's call and it's the final decision. As usual, I do not agree with the solution of the solver.

Now let's see what we saw at the showdown

Gutshot and backdoor flush draw on the flop, naked gutshot on the turn, air on the river. Danny and I did the right hero call, we did well, and the solver wins zero.
Along with the hand, Danny sent in a question about which line I like best on the river: a block bet or a check-call . I want to dwell on this in a little more detail. The solver doesn't have a block betting range on this river. For value, I want to bet with hands from and higher and set large, because with them we get value from . Block bet with doesn't make sense. What weaker hands do we want to get paid from? Calling with a nine? With seven? They don't bet too often on the flop either. In general, I would not think about block betting.
I was also wary that Danny offered a choice between block betting and check-calling. Be careful please! Don't box yourself in right away. “On the river I have second pair with decent showdown value, so check-call if not a block bet.” No, you need to think a little differently.
We reviewed the block bet and rejected it. So, we start the hand with a check, but whether it will be a check-call depends on other factors. Just because we have a king does not guarantee a call. The king by itself doesn't mean much. After facing a bet, you need to deconstruct your opponent's range into value and bluffs with different categories of hands, think about how often he will reach the river with the correct solver ranges and repeat the optimal strategy with them on the river so accurately. If we come to the conclusion that Villain is likely to bluff too often, then our king call is appropriate—as well as calling with and . However, if the analysis shows that the opponent bluffs less often, and value bets wider, then our hands with a king turn into a simple fold, and not only with a ten, but also with a queen.
In any case do not go off the absolute strength of the hand in situations where the opponent represents a combination stronger than yours. This is a dangerous trap that many fall into. A hand will never be strong enough to automatically check-call unless it beats some value bets. Don't beat value bets? Do not even block a significant part of them? So you have a bluffcatcher. The decision with a bluffcatcher depends only on how often your opponent bluffs, and the second pair is not fundamentally different from the third.
I hope my commentary is useful to Danny and some of you. Glad I was able to defeat the solver in this hand. Thank you for your attention, see you in the next episodes!











