Let's dig into poker history a bit. Red Chip Poker coach Adam "w34z3l" remembered the theorems that were invented by our ancestors back in the 2000s. According to him, in those wonderful times, these theorems were known to everyone who considered himself a professional. Well, those who knew about these theorems considered themselves professionals.
Adam checked whether this ancient secret knowledge has passed the test of time and whether it can be adapted to modern realities. On the plus side, they are much easier to remember than the correct c-bet frequency in a 3-bet pot, but on the downside, not all of them work flawlessly. However, like all these solvers.
Balug's theorem
This theorem is not about the big fish of the sturgeon family, but about raising on the turn. It was formulated by Andrew BalugaWhale in 2006 on 2+2. It sounds like this:
The strength of one pair should be significantly reassessed after a raise on the turn
Original example from 2006:
We're UTG with Ako, raising to 4bb (you can feel the old-school vibe right away). BTN call, flop comes A93o. We make a pot-sized bet (now the solver advises to bet much less), the opponent calls. The turn is a 7 for a flush draw. We bet the pot again and get raised.
Balug's theorem is that after these raises our top pair with top kicker doesn't look very good. The theorem does not say that you must fold, just that you need to be very critical of the strength of your hand. Well, and sometimes still say “pass”, as quite often this will turn out to be the right decision.
If we analyze this situation in the solver, then it almost always advises calling both a raise on the turn and a bet on the river. However, it should be understood that after betting on the river, our top pair top kicker is just a bluff catcher. The EV of calling on the turn isn't very high, technically it's a call we play to protect our range, otherwise, we end up folding too much on the turn. If in this situation our hand is weaker than TPTK, then the solver will tend to fold.
In general, this theorem is quite far from GTO and is geared more toward an exploit. The idea is that the average opponent doesn't often bluff raise on the turn. If you look at Range Research to see what the NL200 turn is being raised with at PokerStars these days, it looks like this.
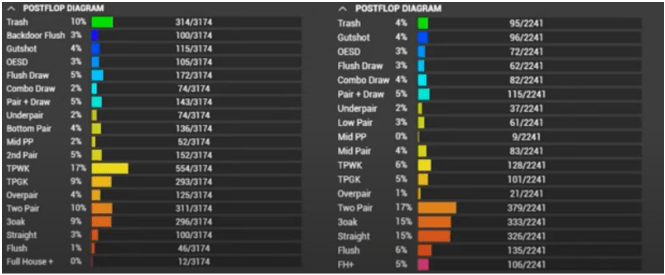
58% of the time the average opponent will have two pair or better after a check raise, and 70% of the time he will have top pair or better. If the opponent is in position, then the value of his hands will be almost half as much – 25% of two pairs and above, and top pairs and above – 30%.
By and large, we can say that Balug's theorem still works. However, keep in mind that it is much more profitable to use it against check-raises since players in position often raise with bluffs and semi-bluffs.
Clarkmeister's theorem
This theorem was also born on 2+2. It sounds like this:
If a fourth suited card comes heads-up on the river and we have the first action, we should bet.
Sounds pretty logical. True, it is quite difficult to prove the benefit or harm of this theorem, since everything here depends on the specific situation.
For example, we are out of position, our opponent c-bets the flop and the turn, and the river comes a fourth flush card. In this situation, our bluff donk bet on the river generates 57% fold equity, and applying the Clarkmeister theorem will be very profitable – if we bet 75% of the pot, then we need to get only 40% of folds to turn this action into profit.
Another scenario that fits the theorem is when we are probing. This is the name of a bet that we place against an opponent who did not place a continuation bet on one or more of the previous streets. Here our bet on the river will already give 62% fold equity. However, this situation is much less revealing, since we almost always have a lot of fold equity here, regardless of the card that hit the river. But in the first case, the fourth card to the flush is just important, since in another situation the donk bet will not be so profitable.
This does not mean, of course, that the theorem works perfectly. If we bet three times out of position, c-betting the flop, turn, and river, in most cases our fold equity on the river will drop to 40%. Moreover, the option in which the fourth card to the flush comes on the river is even worse than the others – in other cases, our fold equity is 45-50%.
Conclusion: Clarkmeister's theorem can be considered working, but not in all situations. GTO is not so optimistic about this theorem and rarely advises betting on the fourth card to a flush.
Yeti theorem
This theorem also arose on 2+2, and received the name in honor of the author.
3-betting on a dry flop, especially a paired flop, is almost certainly a bluff
Let's say we hit the flop A72o or KK2o. Our opponent c-bets, we raise. If he makes another raise, it will be hard to believe in the strength of his hand. In most cases with trips of kings or a set of sevens, upon seeing a raise, almost all opponents will slowplay. But if all the strong hands on dry boards go slowplaying, what does a 3-bet range look like? Is it all bluffs? This looks like a big problem these days. And if you look into the software, it turns out that these days this theorem is simply not true.
Now the average flop 3-bet bluff range player is almost non-existent, and they will only play this way with the stone-cold nuts, regardless of the texture. In a sample with NL200 on a dry or paired board, the percentage of bluff 3-bets and merges is extremely low.
Conclusion: The Yeti Theorem has not passed the test of time. There is a suspicion that even in 2005 it was not exactly printing money ...
Zeebo's theorem
No player is capable of folding a full house, regardless of street or bet size.
Here, even without analysis, we can say that this is a fairy tale. In the right situation, getting rid of a full house is not so difficult, there are such players, and there are many of them. Especially when there are two pair on the board, and we have a low full house.
For example, take the board 8877x. If we have 7x and Villain is betting a lot, folding in this situation can be considered. However, this does not make the theorem useless. To paraphrase it a little, it can serve well now:
Don't try to force players out of the pot if you suspect they have a strong hand.
If you assume that your opponent has a full house, then you should not bluff. This goes for both straights and flushes unless there is history that allows you to believe that your opponent is capable of difficult folds. This is definitely not a situation where you can win money.
Another relevant lesson we can learn from this theorem is that an unknown player is more likely to overestimate the strength of his hand. Someone will look at their cards and think: “Wow, I have a full house!” Even if this full house is dominated by all sides, they will rely on the absolute strength of their hand, not paying attention to everything else. Even today, there are plenty of such players at the tables, especially at the micro limits.
AEJones theorem
It was published by high roller Aaron "aejones" Jones on the 2+2 forum in 2007.
Nobody ever has anything.
Of course, this wisdom of past centuries should not be taken literally, but this theorem can be rephrased as follows:
Players won't always have as strong a hand as you think.
This problem can be called the "monster under the bed" syndrome. It usually escalates during downswings, when you constantly think your opponent has the nuts. “Of course, we caught a low set, but the enemy must have top set!” It is not difficult to believe this, especially if these situations have happened to you quite often over the past few tens of thousands of hands.
If we try to abstract away the effect of streaks and look at the big picture, it turns out that the opponent's hand is quite often weaker than we thought. It's not that easy to make a strong hand in hold'em, and if we don't always succeed, then our opponents must have the same problem. It is useful to remember this, especially during a downswing.
From this statement, one more can be deduced, which does not lose its relevance at all times:
Aggressive play is much more profitable than passive play.
Don't worry too much about the fact that your opponent has a strong hand in some particular cases because this can prevent you from deciding on a profitable bluff at the next table. And sometimes you might even be surprised how easily opponents are willing to part with their cards.
That's all for the ancient theorems. I hope you've enjoyed our trip down memory lane, and what the hell, maybe you've even learned something from talking about the principles that were considered unshakable in the old era of online poker.











