Today we analyze an interesting hand played in the first Poker Go Cup tournament by two famous high-stakes professionals Alex Foxen and Adrian Mateos.

We are at the final table, five players remain in the game. It's folded to Foxes and he raises with for just over three big blinds. Mateos defends with .

To analyze the pre-flop action, we ran a quick simulation, taking into account the sizings used and the payouts on the final table. The solver confirmed that the actions of both players are standard. The small blind's raising range is full of strong pocket pairs and broadways, and many medium-strength suited hands are called.

The big blind basically chooses between calling and folding. He can also three-bet the strongest hands and junk with blockers.

Of course, the ranges of these players will differ from those calculated by us, because even if the players had studied this situation specifically, it is beyond human strength to remember the solver ranges exactly.
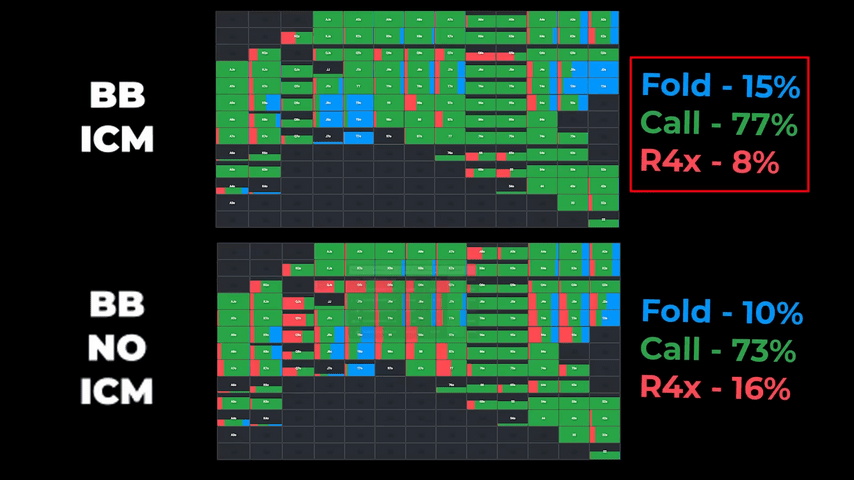
Our calculations allow us to understand a little better the impact of ICM on the decisions of players. Even when the player's stack in the small blind is larger, they still open a little more passively than allowed by chipEV. And when the larger stack belongs to the big blind, the small blind strategy becomes as conservative as possible.

The optimal BB game under the influence of ICM also deviates quite a lot from the optimal play.

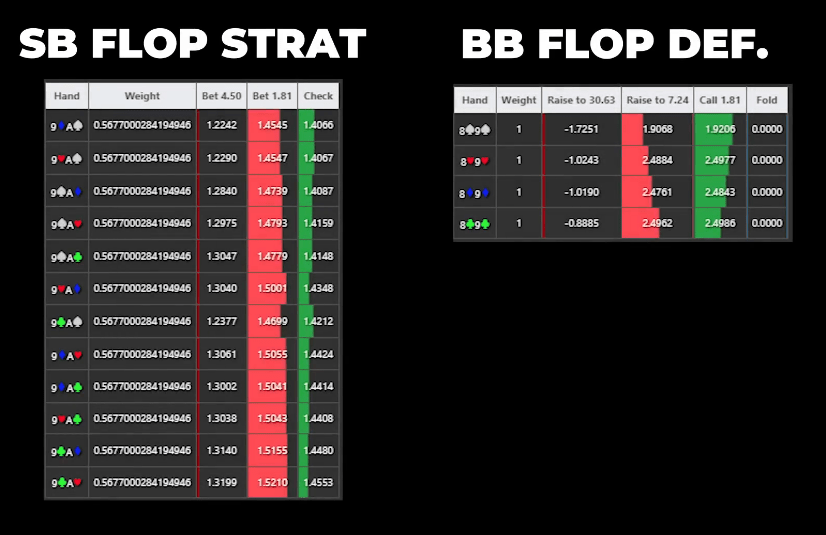
On the flop, Foxen c-bets with Ace-high and Mateos calls with a gutshot.

The solver approves of both their decisions.
Now let's look at the difference in the post-flop play with and without ICM.
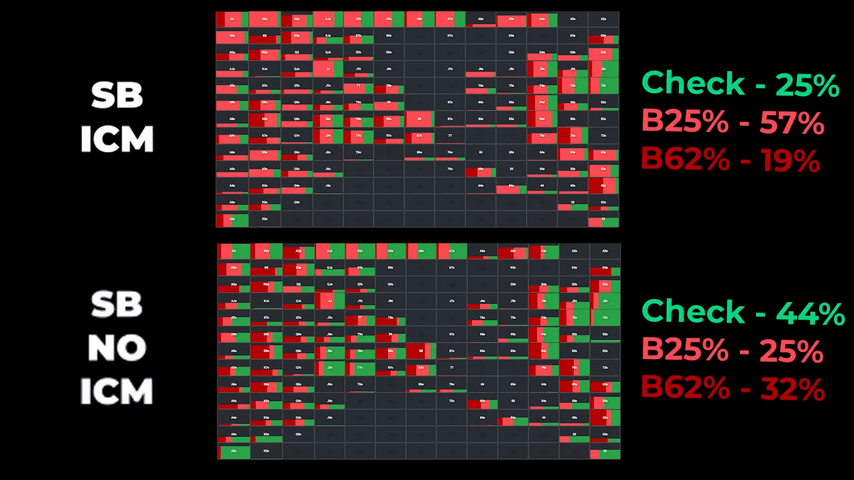
Without the influence of the tournament payouts, the solver checks from the small blind almost twice as often, and when he bets, he prefers the big sizing. In a tournament setting, the big blind is more likely to fold, given the small stack on the button (12.5bb). However, the difference between the strategies is not so great.
The turn is a deuce of diamonds, and Foxen decides to slow down.

The solver completely agrees with him. In its opinion, 100% of Ace-high hands with no other draws, as well as low pairs, should check. They are superior to some of the opponent's hands and inferior to the other part, so they are not interested in inflating the pot.
After seeing the check, Mateos decides to launch a counterattack with his gutshot. The solver considers both actions possible – both bet and check.
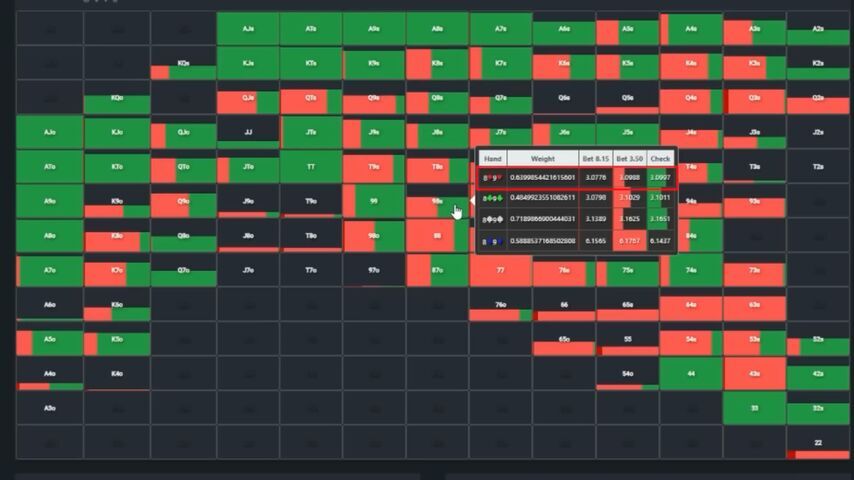
Foxen calls.

According to the solver, this solution can also be mixed. You can't fold all the Ace-highs, but you can't call with every one either.
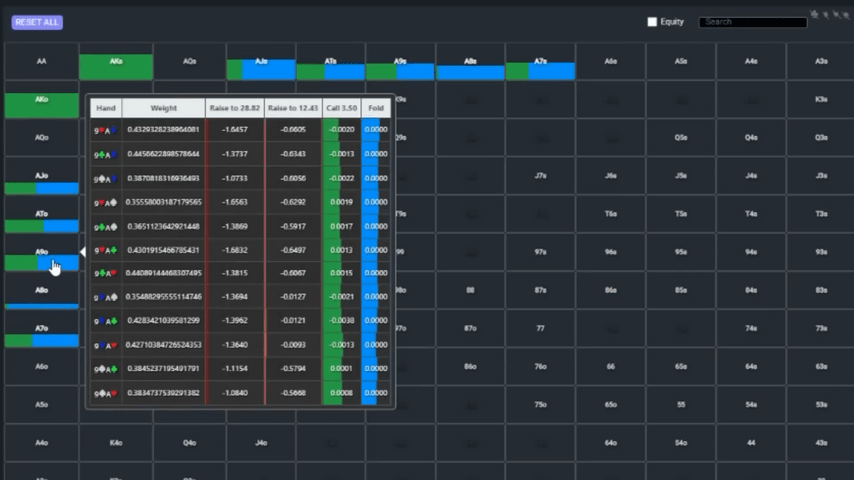
Ace-nine has showdown value in heads-up play. Foxen’s hand also blocks not many of the villains’ bluffs. In general, the call can be considered logical. The river brings another deuce. Foxen checks and Mateos finished with a bet that’s about 80% of the pot.

And this is the first time in the calculation tree in which one of the two players does not play by the solver!
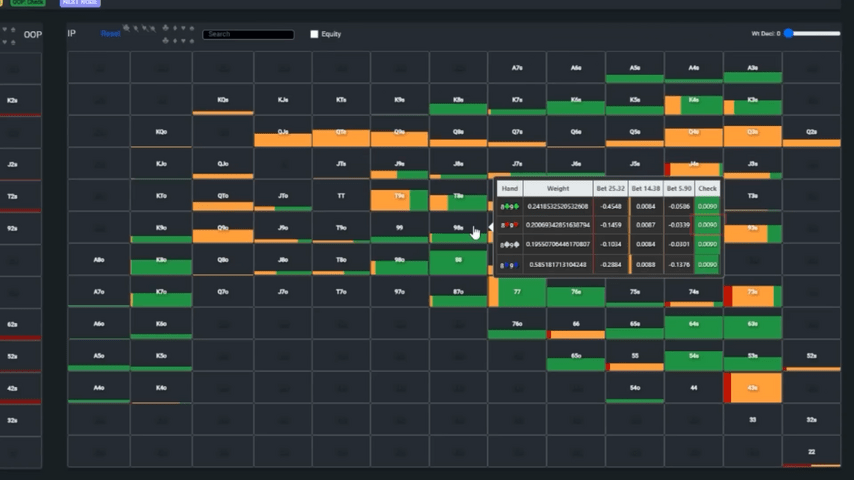
Before branding Mateos a regular bluffer, let's try to figure out why the solver doesn't want to continue bluffing his hand. Perhaps the player made only a small mistake.
The first question is whether this class of hands has a reason to bluff. The answer is obviously yes. The equity of all unmade hands in Mateo's range, including King-high, is zero since Foxen has no hands weaker than Ace-high after check-calling. All weaker hands either fired a second barrel on the turn or gave up.
Given that the EV after checking is zero, weak combinations in Mateos's range need only show any plus in the bluff line in order to prefer the bluff. The choice of bluffing hands is built on the basis of blockers: it is desirable to use cards that increase the likelihood of an opponent folding.
Since most of the time, Foxen should fold Ace-high, especially Ace-King, hands with an ace or a king, Mateos should check. With this, everything is simple. Difficulties begin with hands weaker than King-high.

Solver likes to bluff with and , and check , , and . It’s not because 3s and 4s block the straight since Foxen doesn't have straights in that line, but there are other combinations he will check-call with.

In practice, though, it's impossible to know exactly what range Foxen plans to fold with. Also, Mateos's range may not have solver combos like J4s and T4s, in which case he will have to draw bluffs from other sources.
Let's take a step back and look at Mateos's range in general. First, he still has a lot of with which he will definitely bet. Second, bluffing with Ace-high and King-high is undesirable, not because of the showdown value, which is not there, but because these hands block Villain's folding range. Third, we almost certainly have too many missed straight draws and flush draws, and it's not a good idea to double-bluff with each of these hands.
So it comes down to picking a fraction of the missed draws to bluff and fold with the rest. How exactly to choose? Most likely, there is no fundamental difference, because the EV regret for any of these hands when choosing the “wrong” action lies within a couple of percents, that is, it is very close to zero.
In this situation with a hand weaker than King-high, Mateos could well just flip a coin and do as fortune dictates. In this case, its expectation would not differ much from the solver's.
In practice, you can improve your coin strategy a little by bluffing with hands containing a spade: they unlock missed flush draws. We remove all hands with a spade – and the EV regret remaining when choosing between betting and checking drops to 0.1%.

Anyway, Mateos bet, and Foxen, after spending a few extra time chips, eventually made a hard call and was rewarded with a big pot.

At first glance, from a distance, his call is wrong, because the solver folds his hand a hundred percent of the time.
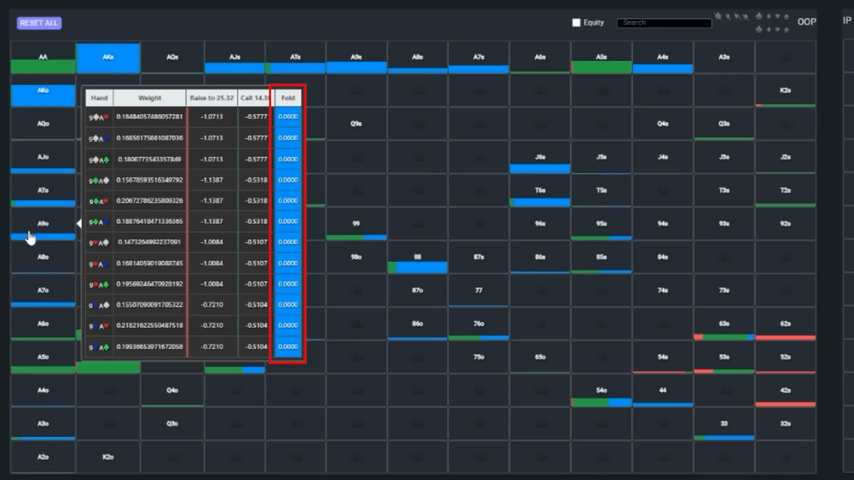
But let's not rush. Keep in mind that ranges on the river are pretty tight, and having just a hand or two of those in the hand, or not, can drastically change the whole strategy.
It's reasonable to assume that Mateos will draw from top pair and bluff with hands weaker than King-high. All of Foxen's hands that fall between them are bluff catchers with the same showdown value. Equity difference between the strongest of them – – and the weakest – – is less than 1%. The choice between calling and folding in such situations is made only with the help of blockers. Since Mateos's drawing range contains not only top pairs but also full houses, the solver prefers to bluff-catch hands with a pair that block the opponent's fulls. , alas, does not fit.
However, that's not all! What if Mateos uses a strategy with more than one sizing on this river? I am not familiar with his game and cannot confidently answer my question, but this is quite possible. If Mateos chooses between pushing just a little more than the pot and sizing in the hand, the small blind's check-call range changes. A blocker for a pair off the board doesn't matter now as the full houses are all-in, and Foxen has to defend some Ace-highs.
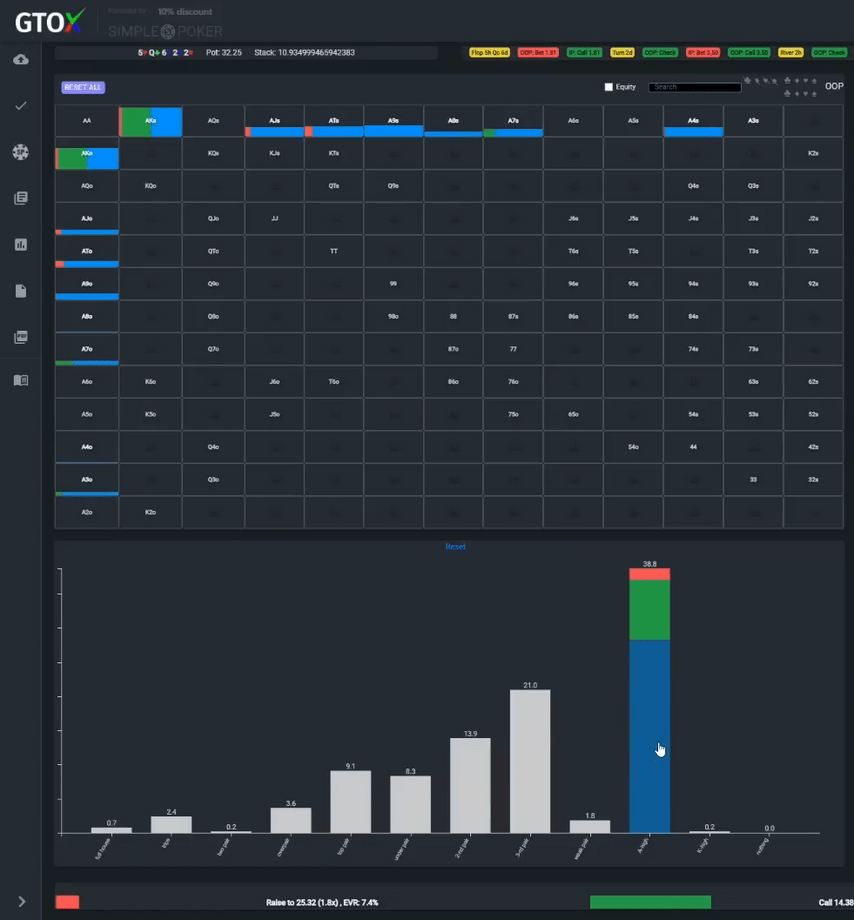
However, in this scenario, Ace-nine offsuit always folds.
Intuitively, this makes sense: it seems odd to bluff with a hand containing a nine, which is part of our opponent's missed straight draws.
Why did Foxen make this call?

We probably don't know. Maybe he saw something suspicious in Mateos’s behavior? Or this option: before calling, Foxen double-checked his cards. Perhaps he decided that Mateos wouldn't bluff with a flush draw that didn't come, and, having specifically a diamond in his hand, made the call. However, if you call according to this logic, the calls will turn out to be too frequent.
In general, whatever one may say, it turns out that, from the point of view of theory, Foxen has more suitable hands to call his opponent. And yet the guy made a hero call and won the most important pot! With that, we congratulate him.
That's all for today. Thank you for your attention and keep the balance.









