Last ace
Imagine that you come to a casino and are offered to play a new game. Perhaps not the most interesting, but here are its rules: the dealer takes the deck in his hands and begins to turn over the cards one by one, and you must guess what the last, fourth ace in the deck will turn out to be. Maybe 25th or 38th – you can indicate any position. The deck is thoroughly mixed, and the distribution of cards is random. Correctly guessing the last Ace pays the same regardless of the position you choose.
It seems difficult to come up with a winning strategy for a game like this since the aces can end up anywhere in a deck like this. However, in reality, we have an optimal choice that will maximize our chances of winning. This choice is
Spoiler:
the last, 52nd card of the deck.
By choosing it, you will win one hundred percent of the time.

Just kidding, of course. You will simply win more often than with any other answer. Let's figure out why.
First of all, there are obviously stupid answers in this game. There is no point in choosing the first three cards because this by definition is impossible. Even if this card is an ace, it will definitely not be the last one in the deck. The ace we need could theoretically come out somewhere between the 4th and 52nd cards.
Let's say you chose the 38th card. In four cases out of 52, you will actually be shown an ace, but the likelihood that it will be the last ace in the deck is not one hundred percent. An important difference between choosing the 52nd card is that by calling it, you guarantee that the ace that comes out in this position will be the last.
To better understand why this is important, let's play with a six-card deck.

The point of moving the choice closer to the end of the deck is that the further we go, the higher the chance the card we choose will be the fourth and final ace. By choosing the fourth card, we win only if the previous three aces were in the first positions. This is not strictly a single layout, because we do not take into account suits. Our aces can come out in any order, so we have 24 winning hands.
But when we choose the fifth card, there are more layouts we need. Aces can be shuffled in the same way, but any position before them or between them can also include any of the two queens. And there will be even more options for our victory when choosing the sixth card.
I don't want to dive into calculations for 52 cards. Here, for example, are all the layouts for a deck of three cards – with two aces and a king.

Obviously, there is no point in choosing the first card – we will never win. Choosing the second card will bring us victory in two cases out of six. The choice of the third card is in four cases out of six. The conclusion is obvious!
Joker jokes
To understand the conditions of this problem, it is enough to know how hand strength is determined in poker. Below I have arranged all the combinations by rank, from royal flush to high card.
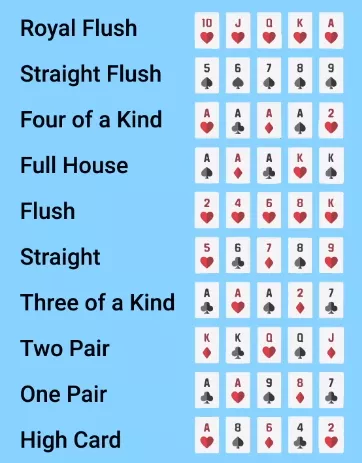
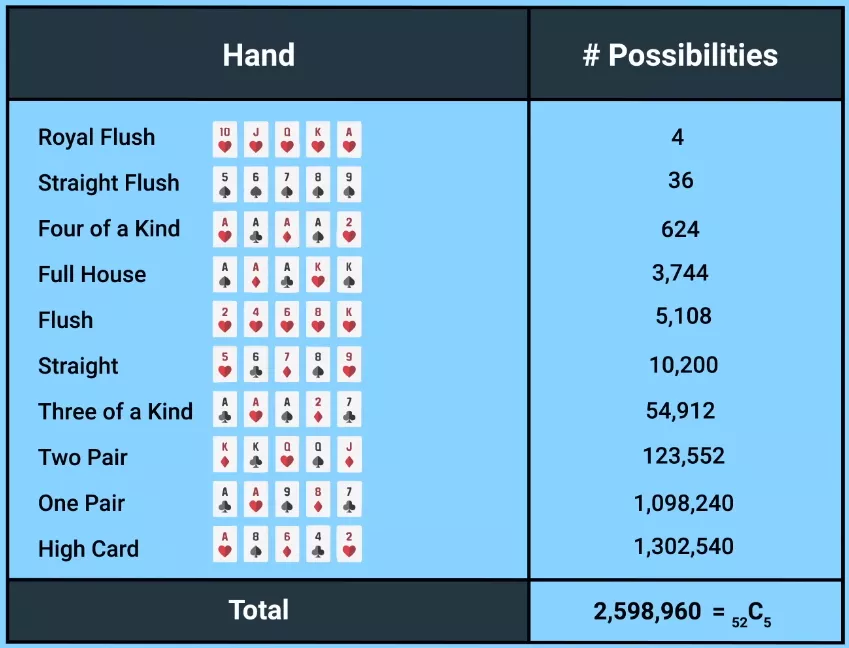
As most of you know, the strength of a combination is determined by the probability of its occurrence: the less frequently it occurs, the stronger it is. There are only four royal flushes, 36 straight flushes, 624 four-of-a-kind combinations, and so on. The total number of combinations exceeds 2.5 million.
Let's imagine that we added a joker to the deck. The deck now has 53 cards instead of 52. Once you receive a joker, you can turn it into absolutely any card. Of course, you will try to strengthen your combination as much as possible. Hand without joker – it's just a pair. With a joker – it's trips if we turned it into . Transforming the joker into also strengthens our hand, but only up to two pairs; but we, of course, choose a stronger combination.
And now my question:
Should the ranking of combinations change when we play with a joker, and if so, how exactly?
Maybe having a joker in the deck will make a flush less likely than a full house? Maybe there will be some other changes? One thing can be said right away: the combination of “five identical cards” appears with the joker. What place in the hierarchy will she occupy?
Obviously, the first: the number of combinations is equal to the number of card values in the deck, 13. There are six times more royal flushes with jokers, and with 24 combinations they will drop to second place.

But we won't have any other new types of hands. So, will the ranking of combinations change because of the joker or not?
I hope you have had time to think about this question because now I will tell you the answer:
Spoiler:
When playing poker with a joker, there is no way to rank combinations according to the probability of their occurrence.
Why is that? Because of the paradox associated with thrips and two pairs.
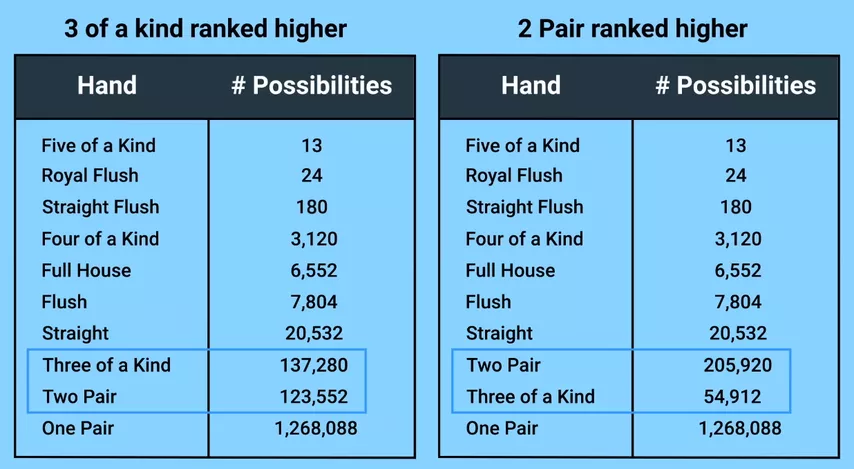
Let's assume we left the order of strength of the combinations unchanged: trips are higher than two pairs. In this case, whenever we are dealt a joker, a pocket pair, and two other cards, we use the joker to strengthen our hand to trips.
Without the joker, trips could be collected 54,912 times. Because of the Joker, their number increased to 137,280.
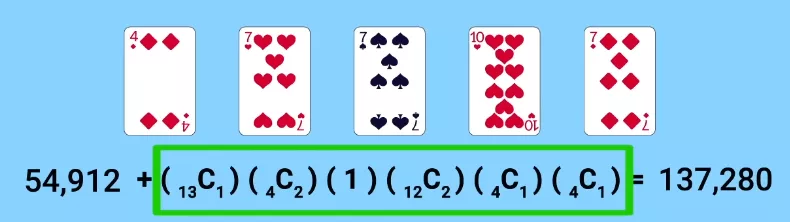
But this is more than the number of possible combinations of two pairs! There were 123,552 of them without a joker, and this number did not change after the introduction of an additional card, because whenever we have the opportunity to make two pairs with it, we prefer trips, and two pairs with a joker always turn into a full house.
Since two pairs are now found less often than trips, the seniority of the combinations has to be changed. But then it becomes unprofitable for players to collect trips using jokers! The number of trips returns to the original 54,912, and the number of two-pair combinations increases to 205,920.
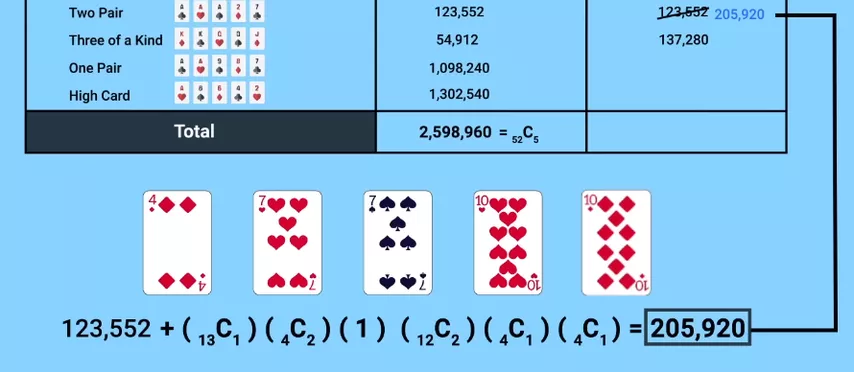
An endless cycle arises, and we come to a paradox: it becomes impossible to finally choose the highest combination based on the probability of its occurrence.
If you are interested, here are the probabilities of combinations when playing with a joker:
Almost fair game
I will show you a game that at first glance looks quite fair, but thanks to a simple algorithm it will allow you to win at least two times out of three, and under favorable conditions – more than seven times to one.
We play with a regular deck of 52 cards, half of which are black and half are red. Two players participate. The first one selects a sequence of three cards, naming their color, for example, “red – red – black”. Then the second player does the same. After that, they begin to draw cards from the deck, and the one whose sequence comes out first wins.
There seems to be no catch. Welcome to the Humble-Nishiyama game!
In October 1969, Walter Penny published a simple coin-flip game in the Journal of Recreational Mathematics. Soon Steve Humble and Yutaka Nishiyama ported his game to a standard deck of cards.
What pitfalls might there be? Well, you probably shouldn't choose a sequence of three identical cards, because the probability of seeing a third red card after two red ones have already come out is slightly reduced. But what else? After all, the chance of getting a black or red card is always about 50/50.
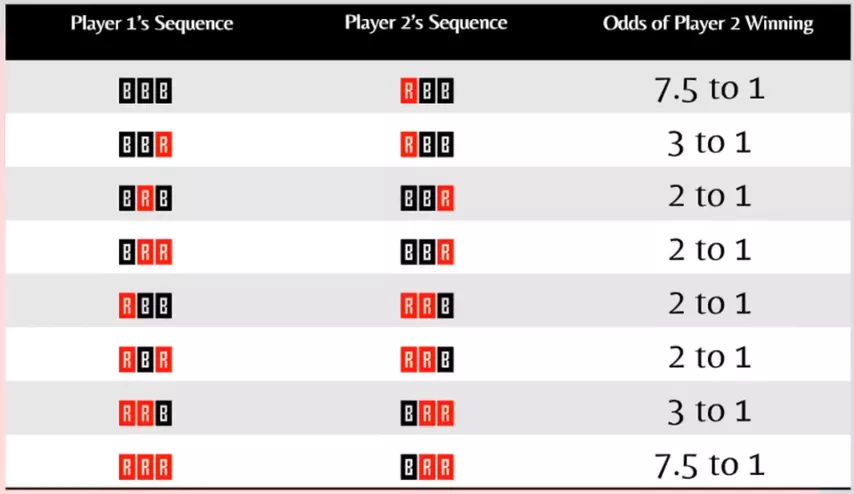
Indeed, if we exclude the monotonous options of RRR and BBB, there is practically no difference for the first player to choose. However, the second one has a working strategy that guarantees victory.
Let's say the first player chose BRB. We take the second card of its sequence, change the color, put it at the beginning, remove the last card – and the adjustment is ready:

Our advantage over the first player is more convincing than the innocent fun of random distribution of cards might suggest:
And it exists because this game belongs to the class of intransitive ones.
Example of transitivity:
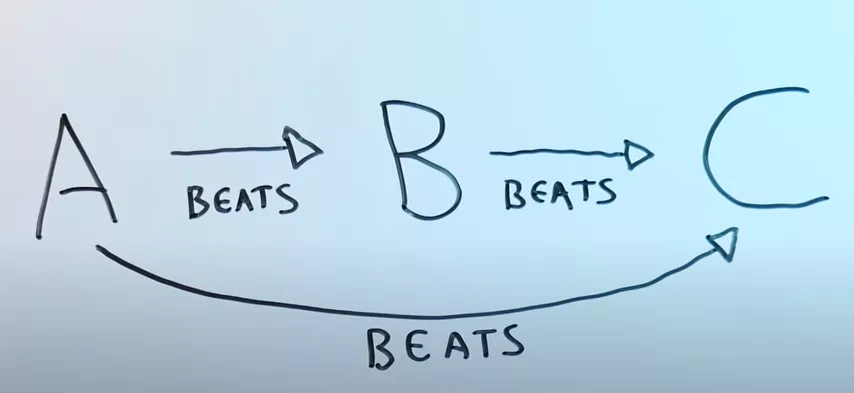
If you like pizza better than tacos, and you prefer tacos to canned dog food, then when choosing between pizza and canned dog food, you will also vote for pizza. Such food preferences will be transitive. However, if for some unknown reason dog food tastes better to you than pizza (but only in this pair!), your food preferences will be intransitive.
In nontransitive games, the first player has no better choice. The relations in them describe preferences on pairs of alternatives, the comparison of which leads to the presence of cycles: A is preferable to B, B is preferable to C, and C is preferable to A. The classic example is, of course, rock, paper, scissors. This game creates a cycle of possible choices, none of which provide the best chance of winning.
The Humble-Nishiyama game is also intransitive. Here is the hierarchy of loops in this game:
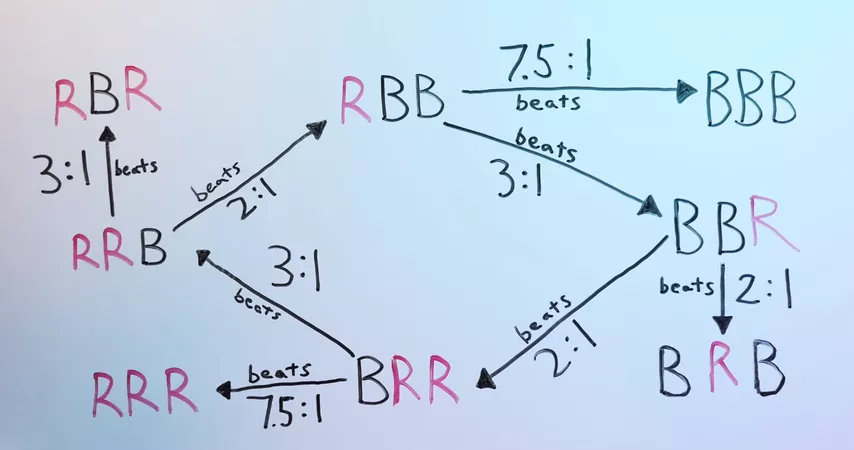
Knowing the first player's choice, we can choose the most profitable answer. And the game, which at first glance seemed so fair, actually gives the second player a huge advantage.















