The rules of poker are very simple and can be learned in a few minutes. Beginners need to remember the ranking of hands, positions, and the sequence of betting rounds.
When learning more about poker and delving deeper, it surprises some players that some of the concepts are based on complex mathematical theories. You don't need to know them thoroughly for successful results, but it is useful to have some idea about them or read a summary. One such concept is game theory.
What is Game Theory?
Game theory is a branch of mathematical economics whose main task is to analyze the strategies of players and resolve conflicts between them.
Game theory is used not only in economics, but also in other sciences such as sociology, biology, and cybernetics. It is also used in poker. Conflict refers to a struggle for a desired outcome between two or more players. Each opponent, within the framework of the situation, takes actions to achieve a result. The sum of the reactions of all opponents creates the final outcome, which is called the payoff. It can be positive or negative.
In the early 50s, John Nash developed methods of analysis for game theory. The work he did eventually acquired practical uses and real-world applications. The main idea of John Nash's formula is the idea of an optimal strategy for players, where their actions aimed at maximizing their own payoffs lead to an improvement in the situation for all participants. In the process, the rivals establish an equal situation known as the "Nash equilibrium."
What is the Meaning of Nash Equilibrium?
The Nash equilibrium, a key concept in game theory developed by mathematician John Nash, describes a situation where no player can improve their payoff by unilaterally changing their strategy while other players keep their strategies unchanged.
In this state, each player's strategy is optimal given the strategies of the other players.
In the prisoner's dilemma, two prisoners are separately offered a deal to betray the other. The Nash equilibrium is for both prisoners to betray, even though they would get a better outcome if both stayed silent. This is because regardless of what the other prisoner chooses, betraying always results in a reduced sentence for the individual.
If both prisoners betray, they each serve 2 years. If one betrays and the other stays silent, the betrayer goes free while the other serves 3 years. If both stay silent, they each serve 1 year. Betraying is always the optimal choice from an individual perspective, so mutual betrayal is the Nash equilibrium – an outcome where no player can improve their result by changing strategy.
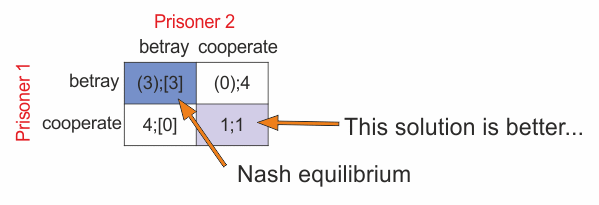
Nash equilibrium is reached when both choose to betray as it leads to the best individual outcome, even though remaining silent would be better for both.
Using this idea, we can discover optimal strategies for live and online poker.
Nash Equilibrium in Poker
The concept is actively used in poker, including when playing MTTs, Sit&Gos, and Spin&Gos. For example, it is useful at the push/fold stage. It allows you to act optimally against unknown opponents, that is, in an information vacuum. It is also valued among novice tournament players because it provides a simple and universal plan of action in hands.
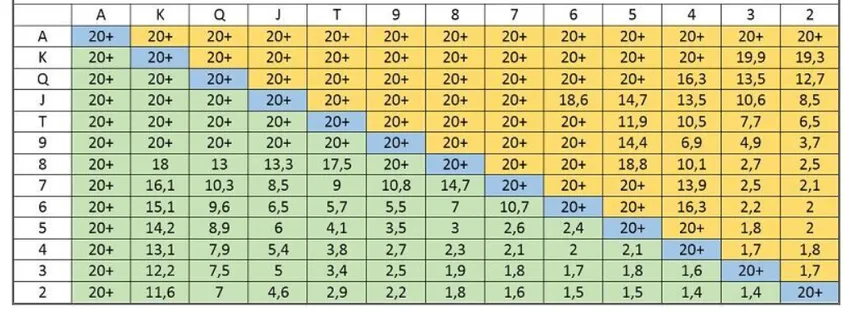
The Nash equilibrium also suggests situations for calling.
A direct consequence of the non-ideal strategies of opponents is the emergence of "pure" and "mixed" strategies. If the game takes place in full accordance with equilibrium, then this is a pure strategy. If some opponents adhere to it or use it only in certain cases, then we are talking about a mixed strategy.
When is the Strategy Optimal?
Even at the final table of the Sunday Million or the WSOP Main Event, opponents are not playing game theory optimally. Only machines play perfectly; real people constantly deviate from the equilibrium. This reduces the effectiveness of the Nash equilibrium but increases the importance of adjusting to your opponents and exploiting their mistakes.
In push/fold situations, players use the equilibrium when the effective stack depth is 15 big blinds or lower. In practice, it is used like this: let's say that after the next increase in blind levels, the effective stack is 13 BB. We are dealt J9o, we look at the table, see a hand in the pushing range, and go all-in. From a mathematical point of view, we made the right decision.
Nash's concept may contradict the Independent Chip Model (ICM). Let's take this situation as an example:
- There are 3 participants left in the tournament, and only two get prizes.
- We have 6,500 chips in our stack and are in the small blind.
- The big blind is the chip leader with 8,485 chips.
- There is a short stack sitting on the button with only 15 chips.
- The blinds are at 400/800.
Preflop, we are dealt a pair of Queens. The button folds.
We have a little more than 8 BB in our stack, and the Nash table clearly indicates that pushing all-in is profitable. Should we strictly follow it and risk our tournament life? Mathematically, yes. In a real situation, this is an easy fold for us, even with pocket aces. The reason is that if we lose to the big blind, we will lose an almost guaranteed payout and give the victory to the short stack. Here, we have to prioritize the work of ICM over Nash equilibrium.
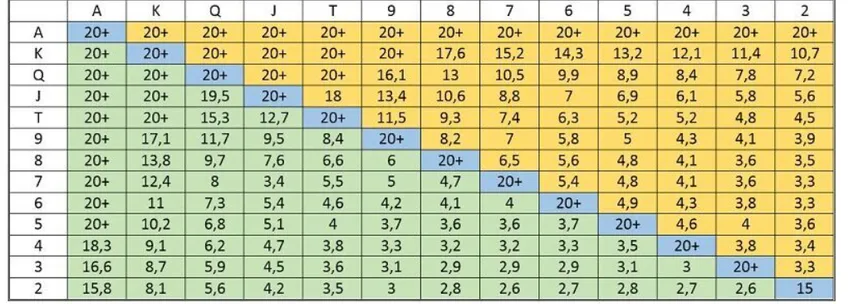
The conflict between concepts is most clearly visible in satellite tournaments. Usually, such tournaments offer tickets to major events as prizes. The final place and number of chips do not matter. In these situations, you often have to fold even the best hands if there is a good chance to book a win without participating in the hand at all.
What is ICM or Independent Chip Model?
ICM is the most important formula in tournament poker. It shows the difference in value between won and lost chips. You can use a free online ICM calculator to do find the ICM, but read this short summary first:
Let's say that in the first hand of a $20 tournament, we have the opportunity to bust out or double up. If we lose, we lose our full stack of 3,000 chips. They cost us the same twenty dollars. But winning and having a stack of 6,000 chips increases our chances of ultimate success, but will not bring a guaranteed $40.
The ICM model demonstrates that the number of chips is not equivalent to their value. It is based on the Nash equilibrium but takes into account additional factors: prize distribution, actions, and the probability of opponents being eliminated. It serves as a tool for determining the size of payouts depending on the number of chips held by the remaining participants.
The main rule of tournament poker is that won chips are always cheaper than lost ones. This is because for first place, you will not receive the sum of all participants' buy-ins, but only the first-place prize. To better understand the concept of ICM, beginners are recommended to use a calculator. If you visit our free ICM tool, you can scroll down to find out how and why to use it.


















